Aritmetické hry


Úkoly

Výsladky:

  1. Kluzák A vyplul od břehu B1, ujel 500m a střetl se s kluzákem B. Oba kluzáky ujely právě délku jezera. Kluzák A dojel potom k břehu B2 a kluzák B k břehu B1. na zpáteční cestě se oba kluzáky střetly ve vzdálenosti 300 m od břehu B2. Oba kluzáky ujely tudíž celkem vzdálenost, která se rovná trojnásobné délce jezera. Jednu délku jezera ujely oba kluzáky za čas t, 3 délky ujely tudíž za čas 3t. Za čas 3 t ujel kluzák A vzdálenost 3 * 500 m = 1500 m, což je vzdálenost o 300 m větší než délka jezera. Délka jezera je tudíž 1500 - 300 = 1200 (m).
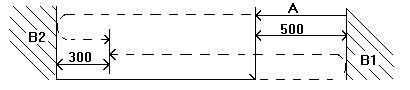
    Od vyplutí kluzáků A i B do jejich prvního střetnutí uplynul stejný čas t. V tomto čase uplaval kluzák A 500 m a kluzák B 700 m. Jelikož dráhy jsou úměrné rychlostem a časům, platí 500 = v1 * t, 700 = v2 * t, z toho 500/700 = v1*t/v2*t a z toho v1/v2 = 5/7.
    Poměr rychlostí se rovná poměrům drah, které oba kluzáky ujely za tentýž čas t.
    obr


  2. Vyjeli Zůstali na druhém břehu Vrátili se Čekali na převoz
    1. 2 boj. 7 zaj. 1 boj. 7 zaj. 1 boj. 3 boj. 27 zaj.
    2. 2 boj. 7 zaj. 1 boj. 7 zaj. 1 boj. 2 boj. 20 zaj.
    3. 1 boj. 7 zaj. 6 zaj. 1 boj. 1 zaj. 2 boj. 13 zaj.
    4. 2 boj 7 zaj. 1 boj. 7 zaj. 1 boj. 1 boj. 7 zaj.
    5. 2 boj 7 zaj.

  3. V době, kdy začala schůze, byla malá ručička na číselníku hodin mezi číslicemi 6 a 7 a velká ručička mezi číslicemi 9 a 10.
    Označme počet hodin v té době, kdy schůze začala, písmenem x. Tímto písmenem označíme i úhel, který opsala malá ručička na své cestě od čísla 12. Jestliže počet hodin v té době, kdy schůze skončila, označíme písmenem y, označíme i úhel opsaný malou ručičkou ze základní polohy (od dvanácky) do tohoto času písmenem y. Tentýž úhel y opsala velká ručička za dobu od 6.00 h (byla tehdy na dvanáctce) do začátku schůze. Malá ručička, která se pohybuje dvanáctkrát pomaleji, opsala za tutéž dobu od číslice 6 úhel y/12. Dostaneme x = 6 + y/12. Do doby, než schůze skončila, si ručičky vyměnily místo. Usuzujeme podobně a dostaneme: y = 9 + x/12. Řešíme soustavu dvou rovnic a dostaneme: x = 6 114/143 hodiny = 6 hodin 47 minut 49 138/143 sekundy. To je doba, kdy začala schůze. y = 9 81/143 hodiny = 9 hodin 33 minut 23/143 sekundy. To je doba skončení schůze.
  4. Jedna třetina jsou dvě šestiny, půl třetiny je jedna šestina, půl druhé třetiny jsou tudíž tři šestiny, čili jedna polovina. Polovina ze sta je 50.
  5. Včely musí na 1 kg medu nasbírat 2,77 kg nektaru.
  6. Majitel koruny dostal číslo 7 a majitel padesátihaléře číslo 9. Ondřej násobil své číslo dvěma a Toník třemi. Jestliže je součet dělitelný třemi, to znamená, že Ondřej měl číslo 9 a tudíž vlastnil padesátihaléř. Jestliže součet není dělitelý tremi, znamená to, že Ondřej měl číslo 7 a tudíž vlastnil korunu.
  7. Na místě jednotek se vyskytuje nula: 22 222 222krát.
    Na místě desítek se vyskytuje nula: 10 * 2 222 222 = 22 222 220 krát.
    Na místě stovek se vyskytuje nula: 100 * 222 222 = 22 222 200krát.
    atd. Tudíž:
    22 222 222 + 22 222 220 + 22 222 200 + ... + 20 000 000 = 175 308 642.
    Výsledek: V zápisu uvedených čísel se číslo nula vyskytne 174 308 642krát.
  8. Na prvním poli je jedno zrno. Na druhém bude 2 * 1 = 2 zrna, na třetím 2 * 2 = 4, na čtvrtém 2 * 4 = 8 zrn atd., čili
    2, 22, 23, 24, 25, 26, ..., 263 = 9 223 372 036 854 775 808 (zrn).
    Velikost tohoto čísla si můžeme předtavit tak, že si vypočteme, jaký prostor by zaujala zrna, která by ležela na posledním poli šachovnice. Byla by to krychle o délce hrany přibližne 7,48 km. Kalif dal toto množství přepočítat na velbloudí náklady. Velikostí výsledku se úplně vystrašil, neboť naložíme-li na jednoho velblouda 140 kg pšenice a předpokládáme-li, že jeden velbloud potřebuje v "husím pochodu" délku 5 m, karavana s vypočítaným množstvím zrní by byla dlouhá víc než 11 1/2 miliardy kilometrů.
  9. 19 2/7 + 80 45/63; 19 3/6 + 80 28/54; 26 4/5 + 73 18/90; 28 45/60 + 71 3/6 a jiné.

  10. obr
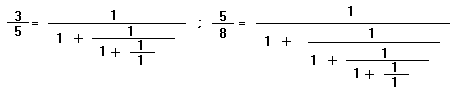
    atd.
  11. Očíslujme si údaje uvedené v úloze:
    1. A a Nitřan jsou lékaři.
    2. P a Bratislavan jsou učitelé
    3. R a komárňan jsou inženýři.
    4. K a F jsou náruživí spotovci, Komárňan nemá o sportu ani ponětí.
    5. Hlohovčan je starší než A.
    6. Trenčíňan je starší než R.
    7. K a Nitřan vystoupili v Leopoldově.
    8. R a Hlohovčan vystoupili v Trnavě.
    Z těchto údajů vyplívají fakta, která hledáme. Např. z I a z II je zřejmé, že A není z Nitry, ale ani z Bratislavy, P není z Bratislavy, ale ani z Nitry atd.
    Sestavme si tabulku všech základních i odvozených údajů tak, že do příslušných polí tabulky ozančíme, kdo odkud není.

    A K R O P F
    Nitřan - - - - - x
    Bratislavan - x - - - -
    Levičan - - x - - -
    Komárňan - - - x - -
    Hlohovčan - - - - x -
    Trenčíňan x - - - - -

    Z tabuly vyplívá, že A je Trenčíňan, K je Z Bratislavy, R z Levice, O je z Komárna, P je z Hlohovce a F je z Nitry. Nyní již lehko určíme i jejich povolání: A a F jsou lékaři, P a K jsou učitelé, R a O jsou inženýři.
  12. Za 1 hodinu přesného času, tj. za 60 minut přesného času, ujdou nástěnné hodiny 58 minut. Za 60 minut podle nástěnných hodin ujdou stolní hodiny 62 minut. Za každou minutu podle nástěnných hodin ujdou ujdou ujdou stloní hodiny 62/60 monuty a za 58 minut podle nástěnných hodin (tj. za 1 hodinu přesného času) 58*62/60 minut. Za 60 minut podle stolních hodin ujd nudík 58 minut. Za každou minutu podle stolních hodin ujde tudíž 58/60 a za 58*62/60 minut podle stolních hodin (tj. za 1 hodinu přesného času) 58*62/60 * 58/60 minut. Za každou minutu podle budíku ujdou náramkové hodinky 62/60 minut. Za 58*62/60 * 58/60 minut podle budíka (tj. za 1 hodinu přesného času) ujdou tudíž náramkové hodinky (58*62*58)/(60*60) * 62/60 minuty. Po výpočtech obdržíme přibližně 59,86 minuty.
    Za každou hodinu přesného času se tudíž náramkové hodinky zpožďují o 0,14 minuty. Za 7 hodin přesného času se tedy zpozdí o 0,14 * 7 = 0,98 což je břibližně o 1 minutu. V 19 hodin přesného času bude tudíž na náramkových hodinkách 18 hodin 59 minut. 

  13.  9 čísel jednociferných       9 míst
90 čísel dvojciferných      180 míst
 x čísel trojciferných      811 míst
                           __________
                           1000 míst
    811 = 810 + 1, 810 (míst) : 3 (cifer.) = 270 čísel
    Posledním ukončeným číslem je číslo 369. Za ním by následovalo 370, z něhož první číslice 3 sojí právě na tisícím místě.
  14. Znázorníme-li věk první z nich úsečkou AB a věk druhé úsečkou CD, úsečka KB znázorňuje, před kolika lety bzlo první tolik let, kolik je druhé dnes. Tehdy však i druhá byla mladší, a to o úsečku ND = KB a její věk je znázorněn úsečkou CN, která se rovná polovině úsečky AB. Z toho vyplývá, že i úsečka MB je dvakrát tak velká jako úsečka KB. Úsečka AB se rovná čtyřem Kb a úsečka CD = 3KB. Až bude druhé přítelkyni tolik let jako je nyní první, bude věk druhé znázorněný úsečkou AB, která se rovná čtyřem úsečkám KB. Avšak i věk první se za tu dobu zvětší o úsečku KB, a bude tudíž znázorněn úsečkou, která se rovná pěti KB. Podle úlohy 4KB + 5KB = 63, takže úsečka KB zobrazuje 7 let. První přítelkyni je nyní 28 let a druhé 21 let. Před sedmi lety bylo druhé 14 let, což je skutečně polovina nynějšího počtu let první přítelkyně.

    obr
  15. Jsou tyto možnosti: 
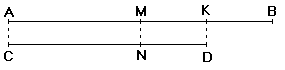
         m:   1   1   1   1   2   3   2   2  
     ž:   1   2   3   4   1   1   2   3,
     d:  24  18  12   6  14   4   8   2.
  16. a) Stačí, jestliže dvojku z konce čísla přesuneme na první místo.
    b)Stačí, jestliže trojku z konce čísla přesuneme na první místo.
  17. Hledané číslo je větší než 10, protože je dvojciferné. Je menší než 23, protože 23 * 4 je číslo trojciferné.
    Hledané číslo je sudé, protože vynásobíme-li ho číslem4,5, dostaneme celé číslo.
    Obrácené číslo je devětkrát větší než polovina daného čísla, to znamená, že obrácené číslo je dělitelné devíti, je devíti dělitelný i jeho ciferný součet; musí být tedy i hledané číslo dělitelnédevíti.
    Hledané číslo je sudé a je dělitelné devíti, je tedy dělitelné i 18.
    Je větší než 10, ale menší než 23, tedy to musí být 18, protože mezi 10 a 23 je to jediné číslo, které je dělitelné osmnácti. 
               18 * 4,5 = 81.
    Na řešení rovnicí je dáno málo podmínek.
  18. Mezi hledanými čísly není číslo 10, protože součin by měl na konci nulu.
    Kdyba všechna hladaná čísla byla větší než 10, byl by jejich součin větší než 10 * 10 * 10* 10, tj. větší než 10 000. Mezi hledanými musí být proto i čísla menší než 10.
    Podle podmínky úlohy se hledaná čísla od sebe liší o jednotku. Zjistili jsme, že alespoň jedno z hledaných čísel je menší než 10, a protože ani jedno se nemůže rovnat 10, čili musí být jednociferná.
    Mezi jednocifernými čísly není číslo 5, protože by muselo být mezi mezi nimi i číslo 4 nebo 6 a součin by končil nulo. Podívejme se na dvě skupiny čísel, která vyhovují podmínkám úlohy:
    1, 2, 3, 4 a 6, 7, 8, 9.
    První skupina odpadá, protože 1 * 2 * 3 * 4 = 24, takže to mohla být jen čísla 6, 7, 8 a 9.§
    Zkouška: 6 * 7 * 8 * 9 = 3024
  19. Účtovali nesprávně. Z 30 Kč, které dali chlapci na nákup, jim 3 Kč vrátil. Nákup tedy stál 25 Kč (za zboží) a 2Kč, jež dali chlapci, tedy 27 Kč. Jestliže z 30 Kč dostali 3 Kč nazpět, skutečně platili (30 - 3) = 27 (Kč).
    Tedy platili 27 Kč, které splo s 3 Kč, jež dostali nazpět, tvoří 30 Kč.
  20. Jestliže na podstavnou část poslední vůle pokládáme poměr mezi matčiným podílem (m) a synovým podílem (s) a dále mezi matčiným podílem a dceřiným podílem (d), vyplívá z toho, že dcera má dostat dvakrát menší podíl než matka, syn zase dvakrát větší než matka. Dědictví je třeba rozdělit na 4 dílů, z nichž 2 díly připadnou matce, 4 díly synovi a 1 díl dceři; m : s : d = 2 : 4 :1.
    Při řešení je možno zaujmout i jiné stanovisko. Závěť je možno vyložit i tak, že chtěl matce zanechat alespoň 1/3 majetku, zatímco podle předchozího výkladu dostala jen 2/7. Syn a dcera si mají rozdělit 2/3 z celého majetku v poměru 4 : 1. Syn by potom dostal (2/15) * 4 = 8/15 a dcera (2/15) * 1 = 2 / 15 celého majetku čili m : s : d = 5 : 8 : 2.
    ze dvou možných řešení, která vyplývají z různého výkladu téže závěti, vyplívá, že závěť nebyla formulována dost jasně. 
  21. 12 * 483 = 5796,     27 *  198 = 5346,
48 * 159 = 7632,     39 *  186 = 7254,
42 * 138 = 5796,      4 * 1738 = 6952,
18 * 297 = 5346,      4 * 1963 = 7852.
  22. Čyřmístné číslo s číslicemi a, b, c, d je možno psát v tvaru 1000a + 100b 10c + d a druhé, které vzniklo přemístěním první číslice na konec čísla, jako 1000b + 100c + 10 d + a. Součet těchto čísel bude: 
        1000a +  100b +  10c +   d
   +    a + 1000b + 100c + 10d
  ______________________________
    1001a + 1100b + 110c + 11d
    Každý sčítanec je dělitelný jedenácti,a proto celé číslo je dělitelné jedenácti.
    Z čísel, která Ondřejovi náhlásili spolužáci, jen číslo 9867 je dělitelné jedenácti, takže bleskově zjistil, kdo počítal správně a kdo nikoli.

Úkoly
* Kurzy * Akcie * Práce * Zájezdy * Zájezdy * Meteobox * Auto *